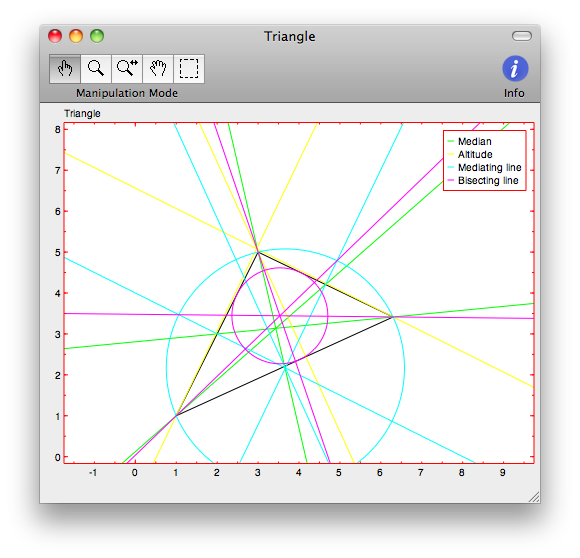
My buddies Frank, Joe, and I had some time to kill today so we decided to build a transistor shunt voltage regulator. We didn’t know correct terminology of the circuit topology at the time, and therefore couldn’t find any examples on the internet. But, we knew the basic topology of the circuit, and had plenty of transistors and zener diodes laying around, so we came up with the circuit shown in Figure 1. Again, we were shooting in the dark, so had to pick out components on gut feel and trial and error, but for a DC sweep to plot input/output characteristics we settled on Rs = 100 Ω, Rl = 470 Ω, a 13 V zener diode, and a 2N2219 NPN transistor.
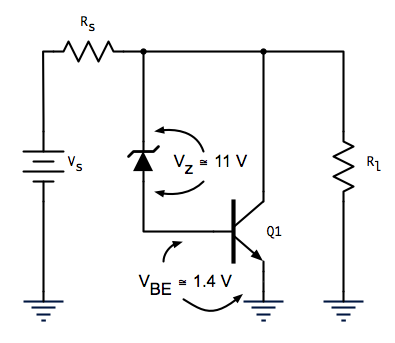 Figure 1—-Transistor Shunt Voltage Regulator
Figure 1—-Transistor Shunt Voltage Regulator
Now, something strange happened when we stepped Vin up from 10—20 V. From Vin = 10—15, Vout increased linearly, just as any voltage divider would. That is, since the zener hadn’t ‘turned on’, the transistor wasn’t sinking any current, and all the current was flowing through Rs and the load. But, when we increased Vin to 16 V, there was a sudden drop in Vout from 12.37 V to 8.50 V. We were puzzled, especially since it appeared as though the circuit was regulating after that, but at a much lower voltage than expected. The end result being plot of Vout/Vin with a strange dip it in (Figure 2). Even weirder, there appeared to be some hysteresis, or memory in the circuit, the plot of the DC sweep from 10—20 V does not match the plot of the sweep from 20—10 V.
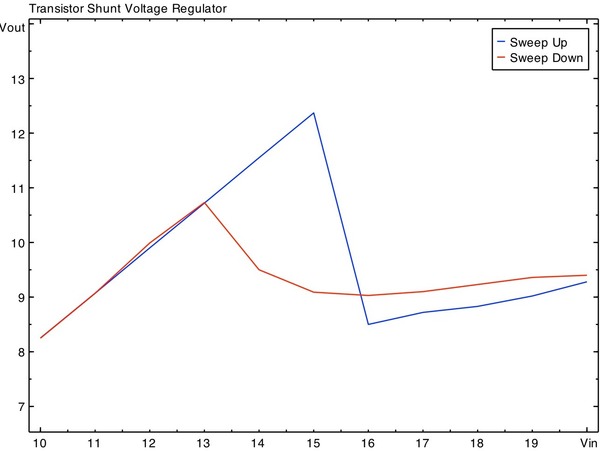 Figure 2—-Original circuit DC sweeps
Figure 2—-Original circuit DC sweeps
In comes our professor, Dr. Amani. He suggested adding some series resistance, in this case a 1k Ω chosen randomly (Figure 3). The result? A a very nice regulating curve (Figure 4), which was nearly identical in both 10—20 V and 20—10 V.
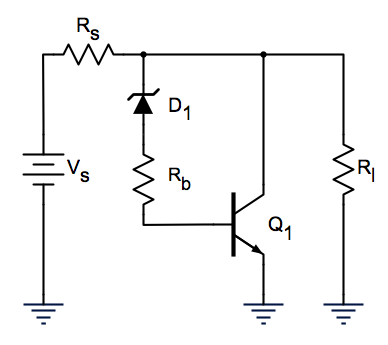 Figure 3—-Rb added to original circuit
Figure 3—-Rb added to original circuit
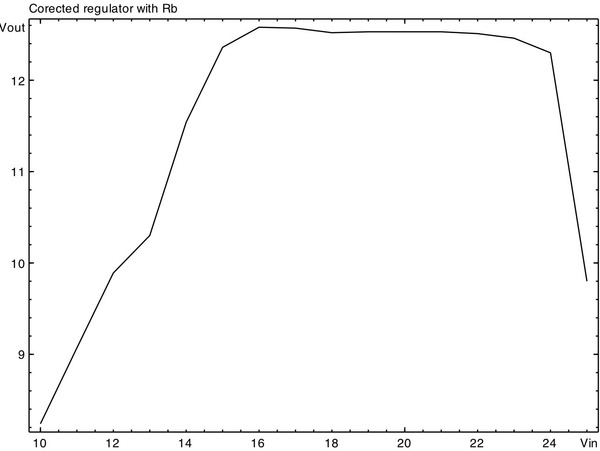 Figure 4—-Correct circuit DC sweep
Figure 4—-Correct circuit DC sweep
Why did the circuit need that resistor? And why did the original circuit have memory? I’m still trying to figure it out.
Download the Sysquake files used to create the plots.

 Share Article
Share Article